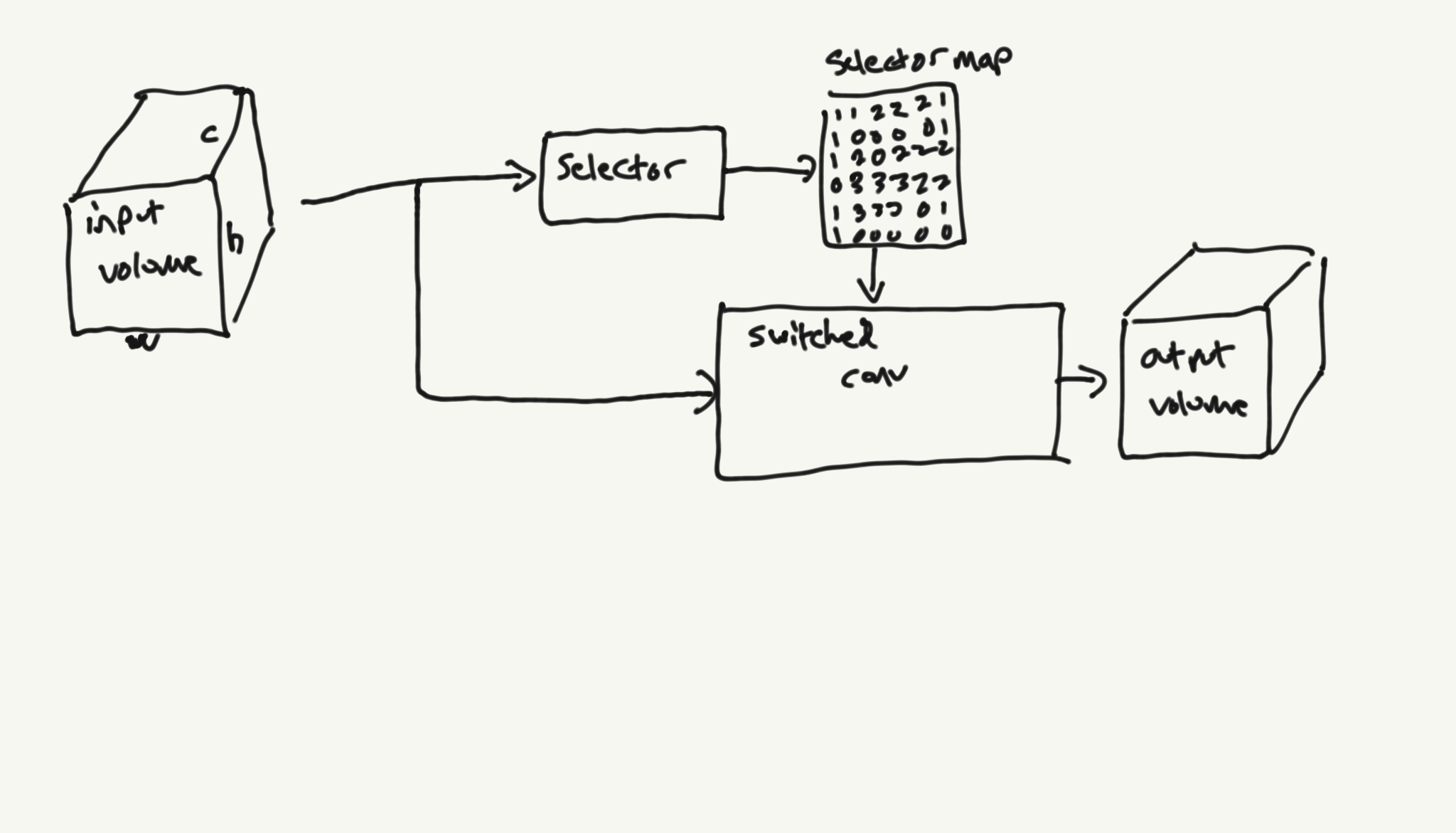
Switched Convolutions – Spatial MoE for Convolutions Abstract I present switched convolutions: a method for scaling the parameter count of convolutions by learning a mapping across the spatial dimension that selects the convolutional kernel to be used at each location. I show how this method can be implemented in a way that has only a…
Category: Super Resolution
SRGANs and Batch Size
Batch size is one of the oldest hyper parameters in SGD, but it doesn’t get enough attention for super-resolution GANs. The problem starts with the fact that most SR algorithms are notorious GPU memory hogs. This is because they generally operate on high-dimensional images at high convolutional filter counts. To put this in context, the…
Training SRFlow in DLAS (and why you shouldn’t)
SRFlow is a really neat adaptation of normalizing flows for the purpose of image super-resolution. It is particularly compelling because it potentially trains SR networks with only a single negative-log-likelihood loss. Thanks to a reference implementation from the authors or the paper, I was able to bring a trainable SRFlow network into DLAS. I’ve had…
Translational Regularization for Image Super Resolution
Abstract Modern image super-resolution techniques generally use multiple losses when training. Many techniques use a GAN loss to aid in producing high-frequency details. This GAN loss comes at a cost of producing high-frequency artifacts and distortions on the source image. In this post, I propose a simple regularization method for reducing those artifacts in any…
Deep Learning Art School (DLAS)
At the beginning of this year, I started working on image super-resolution on a whim: could I update some old analog-TV quality videos I have archived away to look more like modern videos? This has turned out to be a rabbit hole far deeper than I could have imagined. It started out by learning about…
Diving into Super Resolution
After finishing my last project, I wanted to understand generative networks a bit better. In particular, GANs interest me because there doesn’t seem to be much research on them going on in the language modeling space. To build up my GAN chops, I decided to try to figure out image repair and super-resolution. My reasoning…