Switched Convolutions – Spatial MoE for Convolutions
Abstract
I present switched convolutions: a method for scaling the parameter count of convolutions by learning a mapping across the spatial dimension that selects the convolutional kernel to be used at each location. I show how this method can be implemented in a way that has only a small increase in computational complexity. I finally discuss applications of switched convolutions and show that applying them to a pre trained VAE results in large gains in performance.
I have open sourced all of my work on switched convolutions. It can be found here.
Background
Despite the growing popularity of autoregressive models based on Transformers for image processing tasks, CNNs remain the most efficient way to perform image processing.
One disadvantage of CNNs is that it is difficult to effectively scale their parameter count. This is normally done by either increasing the depth of the network or increasing the number of channels in the intermediate states. The problem with scaling either of these numbers is that doing so increases computational complexity by O(n^2) for 2-D convolutions because every parameter is repeatedly applied across every spatial index.
Another option for scaling is to move back to stacked dense layers for processing images. The problem with this approach is it does not encode the translational invariance bias that gives convolutions their prowess at processing diverse images.
In the language modeling space, an interesting idea was put forward by the Mixture of Experts (MoE) paper: scale the parameter count of a model by “deactivating” most of the parameters for any given input. A second paper, “Switch Transformers” extends this idea by proposing modifications that allow a MoE model to scale parameters while achieving a near fixed computational cost. The resulting model is termed “sparse” – it uses the inputs to dynamically select which parameters to use for any given computation and most parameters are unused for every input.
I aim to apply the MoE paradigm to convolutions.
Switched Convolutions
A switched convolution is a convolution which is composed of b independent kernels. Computing the convolution is similar to a standard convolution, except that each spatial input location uses a single one of the b kernels.
Ideally, the mechanism that selects which kernel to use for each spatial location would be learned. I adapt the sparse routing mechanism from Switch Transformers to achieve this, and propose a novel normalization layer that promotes proportional usage of all kernels.
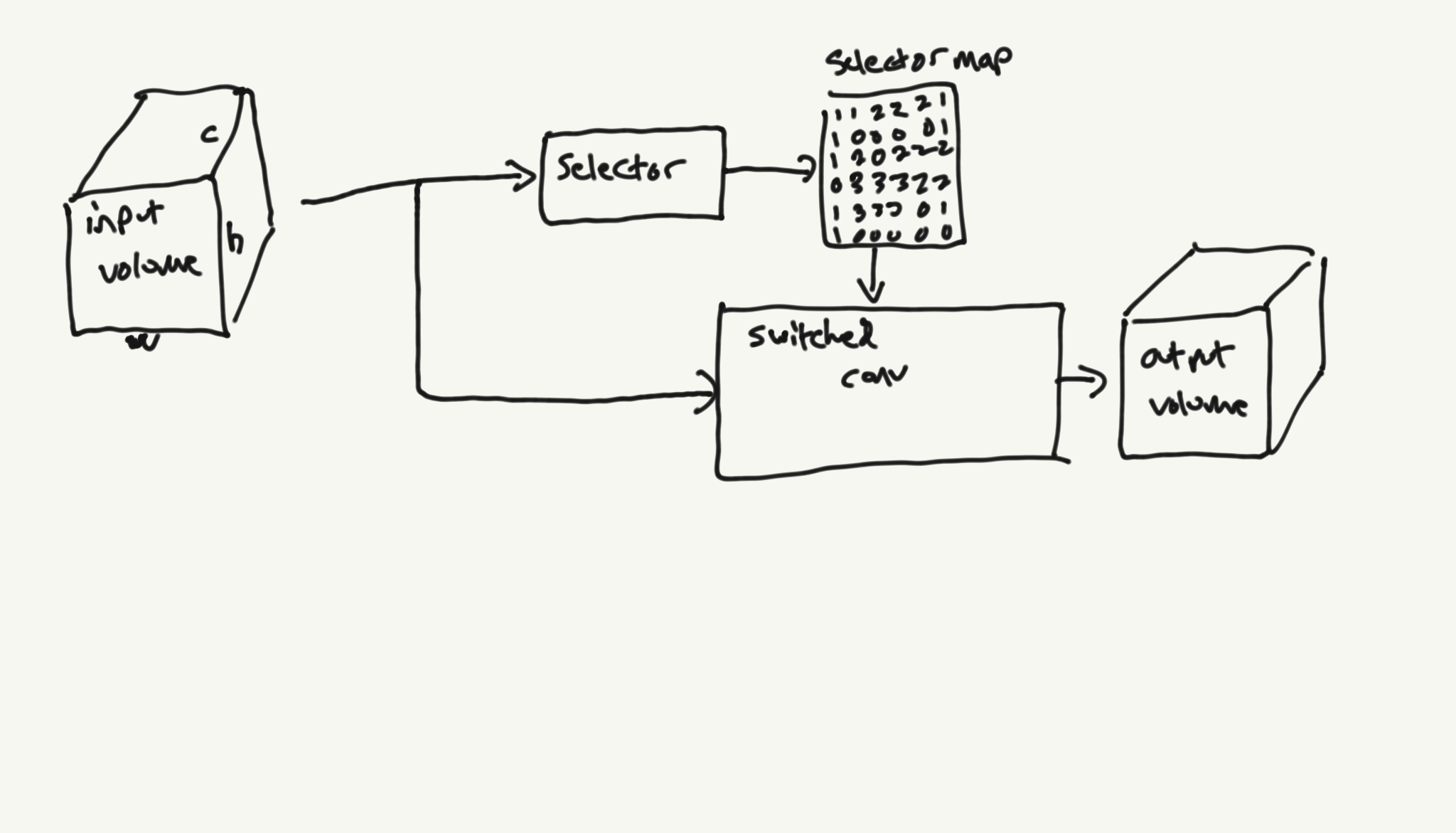
This drawing visualizes how a switched conv works:
Selector
The selector is a parameterized function responsible for producing a discrete mapping from the input space to the kernel selection space. It basically converts an input image into a set of spatially-aligned integers, which will be used to select which convolutional kernel to be used at each image location.
The selector can be attached to any input, but in the experiments discussed in this post, I always attach it to the previous layer in the network. It is worth noting that I have tried using separate networks for generating selector inputs, but they have proven difficult to train and do not produce better results.
Here is a sketch of the internals of a selector:
Switch Processing Network
A NN is embedded within the switch to allow it to segment the image into like zones which will use the same convolutional kernels. It can be useful to think of this network like the dense layers applied to the transformer attention inputs.
The switch NN can be implemented using any type or number of NN layers capable of adjusting the input channel count, for example a 1×1 convolution, a lambda layer or even a transformer.
Switch Norm
The objective of the switch norm is to promote load balancing across all kernels. Without a switch norm, switched convolutions tend to collapse into using a single kernel. The switch norm replaces the load balancing loss proposed in the MoE and Switch Transformers paper. I tried a similar load balancing loss with switched convolutions, but found the normalization method superior.
The switch norm works similar to a batch normalization across the selector dimension, except instead of operating across a batch, it operates across a large accumulated set of outputs, p. Every time the switch norm produces a new output, it adds that output to p. To keep memory in check, the accumulator is implemented as a rotating buffer of size q.
Effectively, this simple norm ensures that the average usage of each kernel across q samples and the entire spatial domain of the input is even. As long as q is big enough, there is still ample room for specialization from the selector, but no one kernel will ever dominate a switched conv.
I used a value of q=256 for most of my experiments. Future work should explore adjusting this hyperparameter as I did not tinker with it much.
It is important to note that the rotating buffer p becomes a parameter for any network using switch normalization. Even though gradients do not flow to it, it develops a characteristic signal over time. Attempting to perform inference without using a saved p always produces poor results.
A reference implementation for the switch norm can be found here.
Differentiable Argmax or Hard Routing
The argmax function, which returns the integer index of the greatest element along the specified axis, is not normally a differentiable function. In implementing switched convolutions, I produce a “differentiable argmax” function.
The forward pass behaves identically to the standard numpy argmax() function. The numeric value of the input that was fed into diff_argmax is recorded.
In the backwards pass, the gradients are first divided by the input recorded by the forward pass. Then, the gradient is set to zero for all but the max element along the specified axis.
The gradients coming out of diff_argmax are a bit odd: they are exceptionally sparse and you might think that entire kernels would “die” off. This is what the switch norm prevents, however.
A reference diffargmax implementation for Pytorch can be found here.
Switched Convolution
The actual switched convolution iterates across each spatial location and uses the output of the selector to determine which convolutional kernel to apply at that location.
Naive Implementation
A simple way to compute the switched convolution output is to perform k standard convolutions for each kernel k, then multiply them by the one-hot output of the selector:
Such a method can even be used without hard routing. In my experiments this does not perform much better than hard routing.
CUDA implementation
It is worth noting that since only one kernel is active per spatial location, the switched convolution only needs to calculate one dot product per spatial location – exactly the same as a standard convolution.
In contrast to Switch Transformers, which require distributed training processes to start seeing a scaling advantage, switched convolutions can be optimized on a single GPU. However, the larger kernel size and pseudo-random access into the kernel has a significant effect on how quickly a switched convolution can run.
A naive CUDA kernel that implements this can be found here. This custom kernel could use a significant amount of optimization (for example, it does not use tensor cores) but currently operates at ~15% the speed of a normal convolution when accounting for both the forward and backward passes with b=8. This means it is net-faster than the naive implementation at b=8, and improves linearly from there. It also has significantly better memory utilization properties because it saves considerably less intermediate tensors for backprop.
Training
Training models with switched convolutions works best with large batch sizes. This makes sense: switched convolutions are very sparse and their parameters will only accrue meaningful gradients across a large set of examples. For example, if b=8, each parameter in the switched conv is generally only receiving about 1/8th of the gradient signal.
While it is possible to train a model incorporating switched convolutions from scratch, it is tedious since the signals that the selector function feeds off of are exceptionally noisy in the early stages of training.
For this reason, I use a different, staged approach to training models with switched convolutions: first, train a standard CNN model. After this has converged, I convert a subset of the convolutions in that model to switched convolutions and continue training. This has several advantages:
- First stage training can be fast: smaller batch sizes can be used alongside simpler computations.
- Since the selector functions are only brought online in the second stage, they start training on fairly “mature” latents.
Converting a standard convolution to a switched convolution is simple: simply copy the kernel parameters across the switch breadth (b) and add a selector. Once you start training, the kernel parameters across the breadth dimension will naturally diverge and specialize as directed by the selector.
Uses & Demonstration
In experimenting with switched convolutions, I have seen the most success in applying them to generative networks. This is intuitive: they offer a way to decouple the expressive nature of the convolution in a generative network from a receptive understanding of what the network is actually working on. For example, a selector can learn to apply different kernels to “draw” hair, eyes, and skin – which all have different textures.
VQVAE
To demonstrate how effective switched convolutions are at improving network performance, I apply them to the stage 1 VQVAE network. I first train a vanilla stage 1 VQVAE to convergence:
I then convert the network by replacing 4 convolutions in both the encoder and decoder with switched convolutions that use b=8 and selector composed of a lambda layer followed by a 1×1 convolution:
The result is a 20% improvement in loss, accounting for both the pixel-MSE reconstruction loss and the commitment loss.
Other Tests
It is worth noting that VQVAE is likely under parameterized for the data I used in this experiment. Inserting switched convolutions in a similar manner into other networks did not show as much success. Here are some notable things I tried:
- Classification networks: inserted switched convs in the upper (high resolution) layers of resnet-50. Performance slightly degraded.
- Segmentation networks: inserted switched convs in the high resolution backbone layers. Performance did not change.
- Stylegan2: inserted switched convs in the generator. Performance degraded. (This is a special case because of the way conv weights interact with the mapping network).
- Super-resolution: A 5-layer deep switched conv network of breadth 8 was found to have competitive performance with the 23-layer deep RRDB network from the paper.
Visualizing the Selector Outputs
It is trivial to output the maps produced by the selectors as a colormap. This can be instructive as it shows how the network learns to partition the images. Here are some example selector maps from the high resolution decoder selector from the VQVAE I trained:
As you can see, these selector maps generally seem to resemble edge detectors in function. They also seem to perform shading in generative networks, for example the arms in the third image.
Future Work
At this point, I don’t believe switched convolutions have demonstrated enough value to support continued research as I have currently formulated them. That being said, I still think the concept has value and I would like to revisit them in the future.
In particular, I am not satisfied with the way the selectors operate. This is purely a heuristic, but I believe the power of switched convs would be best expressed when the semantics of the image are separated from the texture. That is to say – I would have liked to have regions of the image that exhibit different textures (e.g. hair, eyes, skin, background) selected differently.
One project I am currently pondering is working on an unsupervised auto-segmenter. Something in the vein of Pixel-Level Contrastive Learning. If I could train a network that produces useful semantic latents at the per-pixel level, it could likely be applied at the input of the selector in switched convolutions to great effect.