Since joining OpenAI, I’ve had the distinct pleasure of interacting with some of the smartest people on the planet on the subject of generative models. In these conversations, I am often struck by how many different ways there are to “understand” how diffusion works.
I don’t think most folk’s understanding of this paradigm is “right” or “wrong”: they are just different. I think there is a distinct value in having a different viewpoints here: an engineers perspective might be more useful to deploy these things to real products, whereas a mathematicians conceptualization may aid improvements in the core technology.
I’d like to jump through a few of these vantage points in this post, in the hope that I can help more people understand how this amazing technology works.
Compute & Quality
One aspect of generative modeling that has become quite clear to me is that finding principled ways to throw compute at a problem is a surefire way to improve output quality.
This is round-about way of defining the concept of “scaling” in ML. However, when most people think of “scaling”, they think of making bigger models. This isn’t the only game in town, though: you can also scale compute by making a smaller model spend more time iterating on an output. This is exactly what diffusion models do!
Here’s how that works: take a small(ish) model that is capable of doing something extremely simple. For example: remove a microscopic amount of noise from an image. Starting with pure gaussian noise, iteratively apply that model to a series of “images”. Each step, remove the noise predicted by the model. Bam! Lots of compute spent on a single image, and the model can be “pretty small”.

Why does spending compute for quality work, though? Let’s pretend for a second that our ML models are humans (outlandish, I know). When a human sits down to draw a picture, they start with a general concept, e.g. “cat drinking a latte looking tired”. They might start by drawing the outline. Then they might add features (eyes, nose, clothes). Then the background. Then the fur. Next might come some color, one feature at a time. Details are slowly added, little by little. We don’t think of it as such, but we are trading compute for quality. The more time we engage our brains in refining the image, the better the image becomes.
It stands to reason that ML models might be able to exploit this same paradigm, and I think the success of autoregression and diffusion is a strong signal that this might be “the way”.
Gradient Descent at Inference Time
I think we can all agree that the mechanisms of gradient descent are quite magical. At it’s core, it is so simple: compute the derivative of an error function. Use it to make microscopic adjustments to a couple million variables, initialized randomly. Repeat a few thousand times. But the end-result is profound: beat out every expert model humans have come up with in the last century.
What if we went meta on this? What if we trained models that learned the learning process itself? That build error functions from pure text and self optimize? What if I told you that this is what diffusion models are? 🙂
To make this analogy fit, lets pretend that an image is actually a set of neural network weights. We initialize them randomly. We then use a neural network to predict the “update” for these “weights”, conditioned on some text. We take a small step in the direction that the neural network tells us is correct. We repeat this a few hundred times. Out comes an image. Or a MEL spectrogram. Or a latent. Sound familiar?
Means and Modes
ML models are largely statistical beasts, and thus it is often useful to think of them from that perspective. Taking this direction, generative models can be seen as learned mapping functions that morph one statistical distribution (most often gaussian noise) into another (the data distribution). This mapping is generally guided using information like text (called “conditioning information”).
A mapping function like this can learn to predict any statistical property we can formulate a loss function around. The most convenient property to target is the mean of the data distribution, which is modeled with the L2/MSE or L1/MAE loss.
Here lies a problem, though: the mean of many data distributions we might care about is meaningless (pun intended). For example, the mean of the waveforms of all music is close to 0 at all locations. The mean of all RGB pixels is a fuzzy greyish brown blob. Even with a conditioning vector, the mean of all possible “brown dogs walking in the park on pink leashes with sky in the background” images will be a messy blur because many aspects of the above description are unconstrained: where is the dog in the image? Where is the owner? Is there grass and what color is it? A perfect mean of all these factors is a blurry image at best, and more than likely just a solid color gradient; brown to blue.
A more appropriate loss target is the modes of a distribution. A quick refresher on modes:
- The mean of a distribution is the average of all values in that distribution
- The median is the center-most value in the distribution
- The mode is the most frequently occurring value in the distribution
Quick tangent: While the mode is technically the most frequent value of a distribution, what we are really interested in is the “most frequent <n> values in a distribution”. This is much more interesting for generative models since a picture of the same dog is pretty boring, but a picture of every dog breed doing different things that dogs actually do is pretty interesting. When I say “mode” past this point, I am referring to “the most frequent <n> values in a distribution”.
The distributions we are working with exist in an unknowably complicated high-dimensional space. They are inherently multi-modal – which is to say that they contains millions, possibly billions of high density regions which we can consider “modes”. If we could build a generative model that can generate samples from these modes given conditioning information, we’d have something very interesting on our hands!
The trouble with targeting modes for generative models is that they cannot be defined in as a continuous function such that they serve as a good loss function for gradient descent. Instead, you have to target them indirectly.
GANs
You’ve probably heard of GANs, or Generative Adversarial Networks. These types of NNs use a brilliant loss function which results in a generative model that targets the modes of a distribution: a “generator” network maps random noise and a conditioning input to “fake” data. A “discriminator” network classifies inputs as “real” or “fake”. An interplay between these two networks is set up which causes the generator to converge on the modes of the data distribution (since producing samples from these modes would be indistinguishable from the “real” distribution). You’ve probably also heard about the problem with GANs: “mode collapse”. This is when the generator learns to produce samples from a single mode, thus permanently “winning” the game it plays with the discriminator.
W(here)TF are you going with this?
Diffusion models are another clever way of indirectly learning the modes of a distribution! Here’s how you can think of this:
- Given pure noise and a conditioning input, a generator applies a tiny shift in the distribution towards it’s perceived mean (which, as stated above, is likely an amorphous blob of brown/grey colors).
- Given the output of (1), the generator applies another tiny shift in the distribution towards its newly perceived mean, which is now a slightly less amorphous blob of boring color.
- Rinse and repeat (2) until there is no noise left.
Think about what happens as you work through the diffusion process: every time you take a step, you are throwing out potential values that the final image could take on. This changes the distribution and shifts the mean in the process. The result of this process is that the iterative “mean” starts to converge on a “mode”. I’ve sketched this out for you below (the bars in each step are the parts of the distribution getting cut off, the dashed line is the resulting mean):
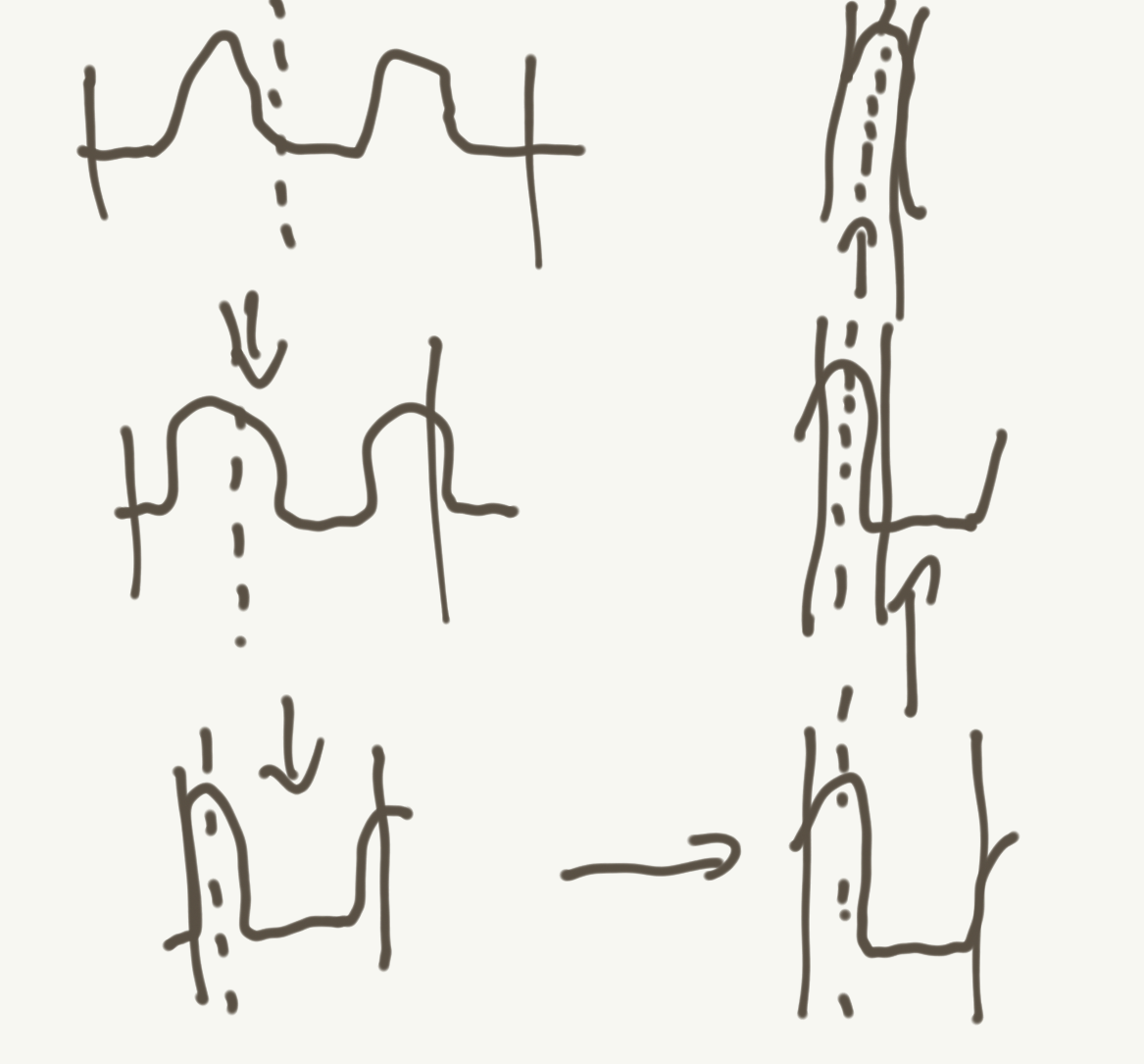
We’ve found a way to optimize for the mean (a totally tractable continuous function), but actually converge on a mode! This is the reason why diffusion models produces such “realistic” outputs: they are mapping noise+conditioning to data elements that actually exist (or should exist) in the underlying data distribution.
BTW – this is also a reason why diffusion models are fairly dangerous to deploy: they have a tendency to “regurgitate” information they have seen in the training dataset. E.g. a face seen too often will become a “mode” that starts to show up in the model outputs. The same goes for artistic styles, voices, musical beats, etc.
Spectral Bands
One interesting way to think about what diffusion is doing is in terms of frequency analysis. Most engineering folks learned in college that all information can be expressed as sums of sine waves of varying frequencies, amplitudes and phases.
The diffusion process can be thought of as recovering these signals, from the low frequencies to the high. Early on, the strong noising means that only vague “details” corresponding to low frequency information emerges. As the process continues, details from the higher frequency bands begin to emerge.
This is a useful way of understanding diffusion because it highlights one of it’s strengths: most generative methods have a propensity to spend too much “time” optimizing high frequency details. Low frequency information only emerges by scaling the models. This is problematic because the human brain works in the opposite direction: we care about semantics (low frequencies) above all else. Who cares how fine a horse’s hair is rendered when it was given 5 legs, for example.
Diffusion not only directly optimizes low frequency details, it also offers us a way to optimize them and measure them: you simply spend more time optimizing the losses in the highly noised quantiles of the diffusion process. This is what OpenAI does with their cosine timestep schedule, as an example.
That’s all I’ve got for now. I’m sure I’m missing a few ways to grok these exciting monstrosities, but I hope you’ve walked away with a few things to think about!